Everything you wanted to know   (and more) about

    PyTorch tensors


Marie-Hélène Burle     

training@westgrid.ca       
January 19, 2022        

Many drawings in this webinar come from the book:

The section on storage is also highly inspired by it

Using tensors locally

You need to have Python & PyTorch installed Additionally, you might want to use an IDE such as elpy if you are an Emacs user, JupyterLab , etc.

Note that PyTorch does not yet support Python 3.10 except in some Linux distributions or on systems where a wheel has been built

For the time being, you might have to use it with Python 3.9

Using tensors on CC clusters

In the cluster terminal:

avail_wheels "torch*" # List available wheels & compatible Python versions
module avail python	  # List available Python versions
module load python/3.9.6             # Load a sensible Python version
virtualenv --no-download env         # Create a virtual env
source env/bin/activate		         # Activate the virtual env
pip install --no-index --upgrade pip # Update pip
pip install --no-index torch		 # Install PyTorch

You can then launch jobs with sbatch or salloc

Leave the virtual env with the command: deactivate

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

ANN do not process information directly

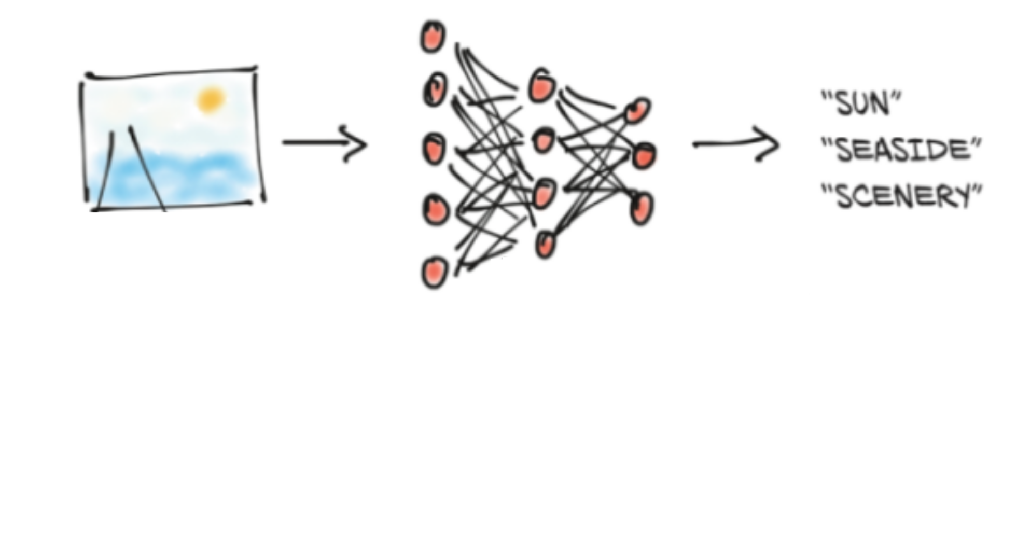
Modified from Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

It needs to be converted to numbers

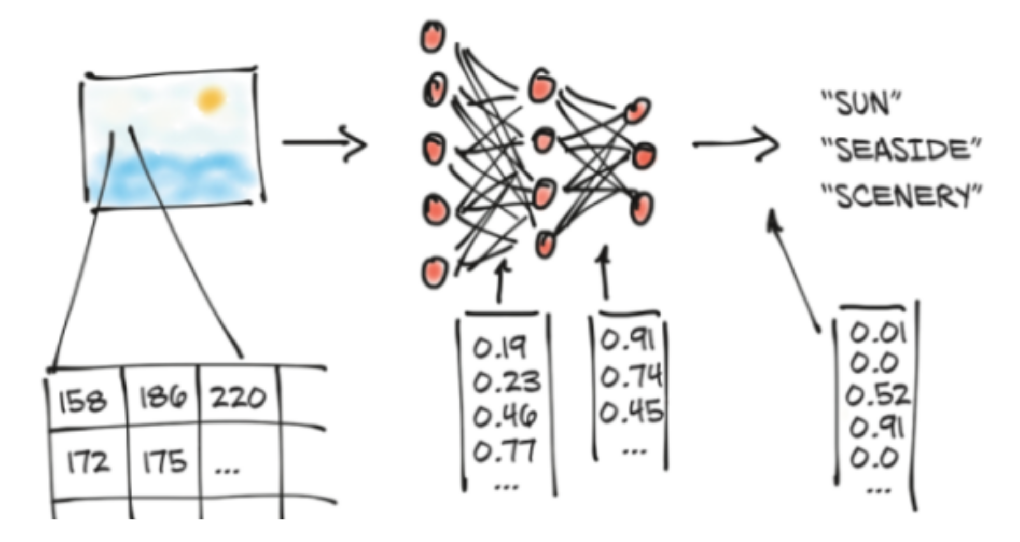
Modified from Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

All these numbers need to be stored
in a data structure

PyTorch tensors are Python objects holding multidimensional arrays

Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

Why a new object when NumPy ndarray already exists?

  • Can run on accelerators (GPUs, TPUs…)

  • Keep track of computation graphs, allowing automatic differentiation

  • Future plan for sharded tensors to run distributed computations

What is a PyTorch tensor?

PyTorch is foremost a deep learning library

In deep learning, the information contained in objects of interest (e.g. images, texts, sounds) is converted to floating-point numbers (e.g. pixel values, token values, frequencies)

As this information is complex, multiple dimensions are required (e.g. two dimensions for the width & height of an image, plus one dimension for the RGB colour channels)

Additionally, items are grouped into batches to be processed together, adding yet another dimension

Multidimensional arrays are thus particularly well suited for deep learning

What is a PyTorch tensor?

Artificial neurons perform basic computations on these tensors

Their number however is huge & computing efficiency is paramount

GPUs/TPUs are particularly well suited to perform many simple operations in parallel

The very popular NumPy library has, at its core, a mature multidimensional array object well integrated into the scientific Python ecosystem

But the PyTorch tensor has additional efficiency characteristics ideal for machine learning & it can be converted to/from NumPy’s ndarray if needed

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

Efficient memory storage

In Python, collections (lists, tuples) are groupings of boxed Python objects

PyTorch tensors & NumPy ndarrays are made of unboxed C numeric types

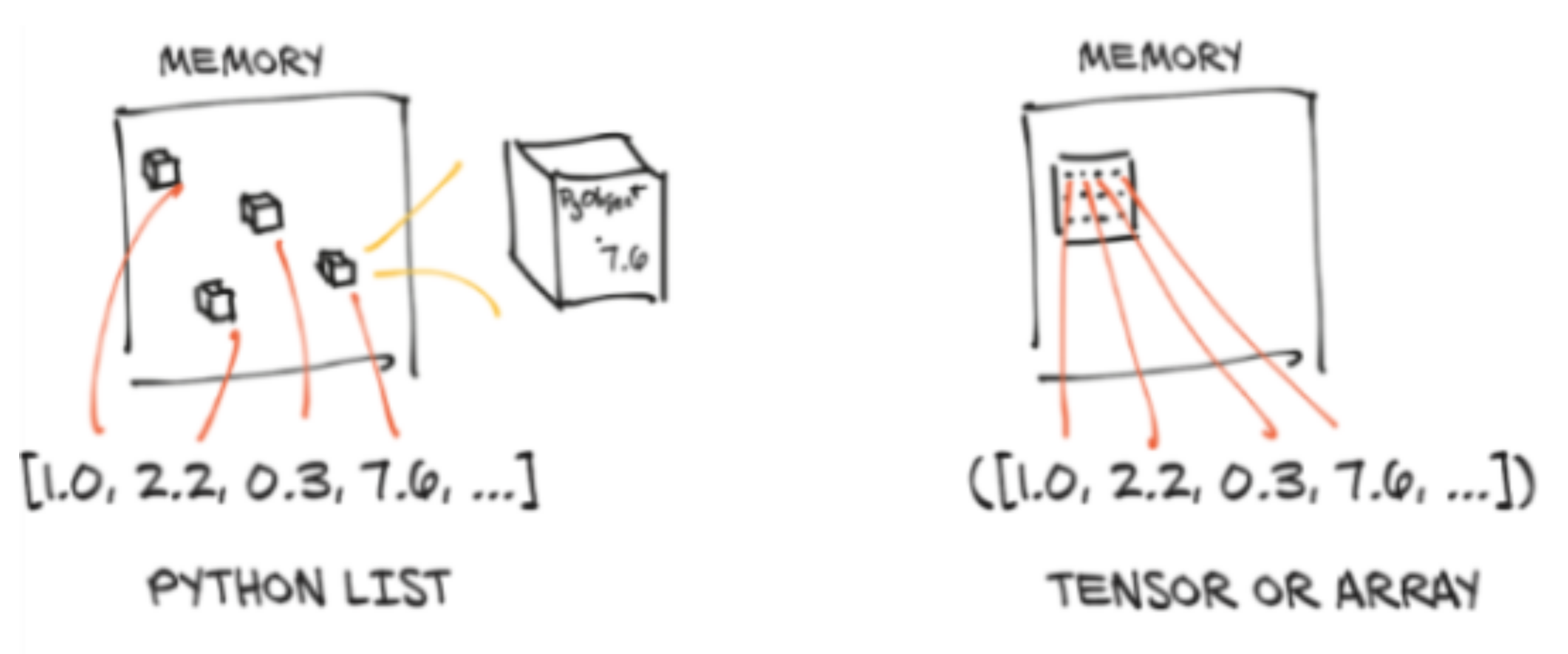
Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

Efficient memory storage

They are usually contiguous memory blocks, but the main difference is that they are unboxed: floats will thus take 4 (32-bit) or 8 (64-bit) bytes each

Boxed values take up more memory
(memory for the pointer + memory for the primitive)

Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

Implementation

Under the hood, the values of a PyTorch tensor are stored as a torch.Storage instance which is a one-dimensional array 

import torch
t = torch.arange(10.).view(2, 5); print(t) # Functions explained later
Output >>>
tensor([[ 0.,  1.,  2., 3.,  4.],
        [ 5.,  6.,  7.,  8.,  9.]])

Implementation

storage = t.storage(); print(storage)
Output >>>
 0.0
 1.0
 2.0
 3.0
 4.0
 5.0
 6.0
 7.0
 8.0
 9.0
[torch.FloatStorage of size 10]

Implementation

The storage can be indexed 

storage[3]
Output >>>
3.0

Implementation

storage[3] = 10.0; print(storage)
Output >>>
 0.0
 1.0
 2.0
 10.0
 4.0
 5.0
 6.0
 7.0
 8.0
 9.0
[torch.FloatStorage of size 10]

Implementation

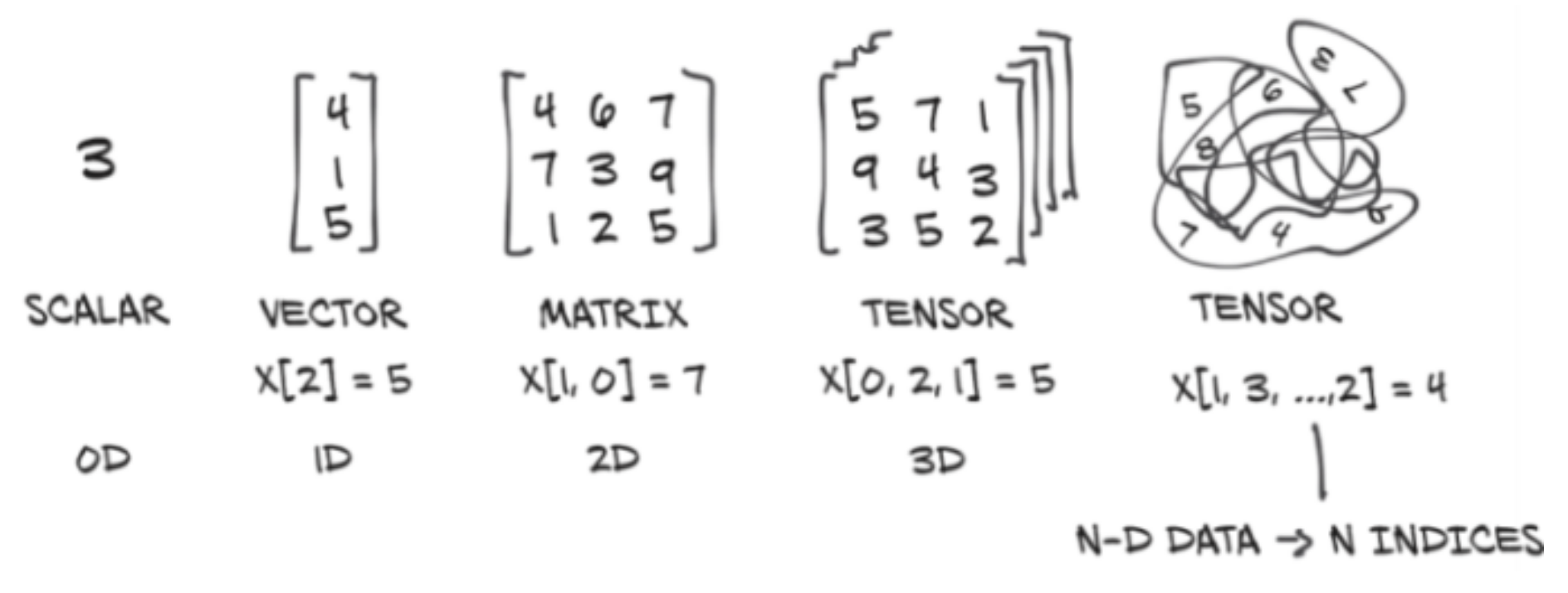
To view a multidimensional array from storage, we need metadata :

  • the size (shape in NumPy) sets the number of elements in each dimension
  • the offset indicates where the first element of the tensor is in the storage
  • the stride establishes the increment between each element

Storage metadata

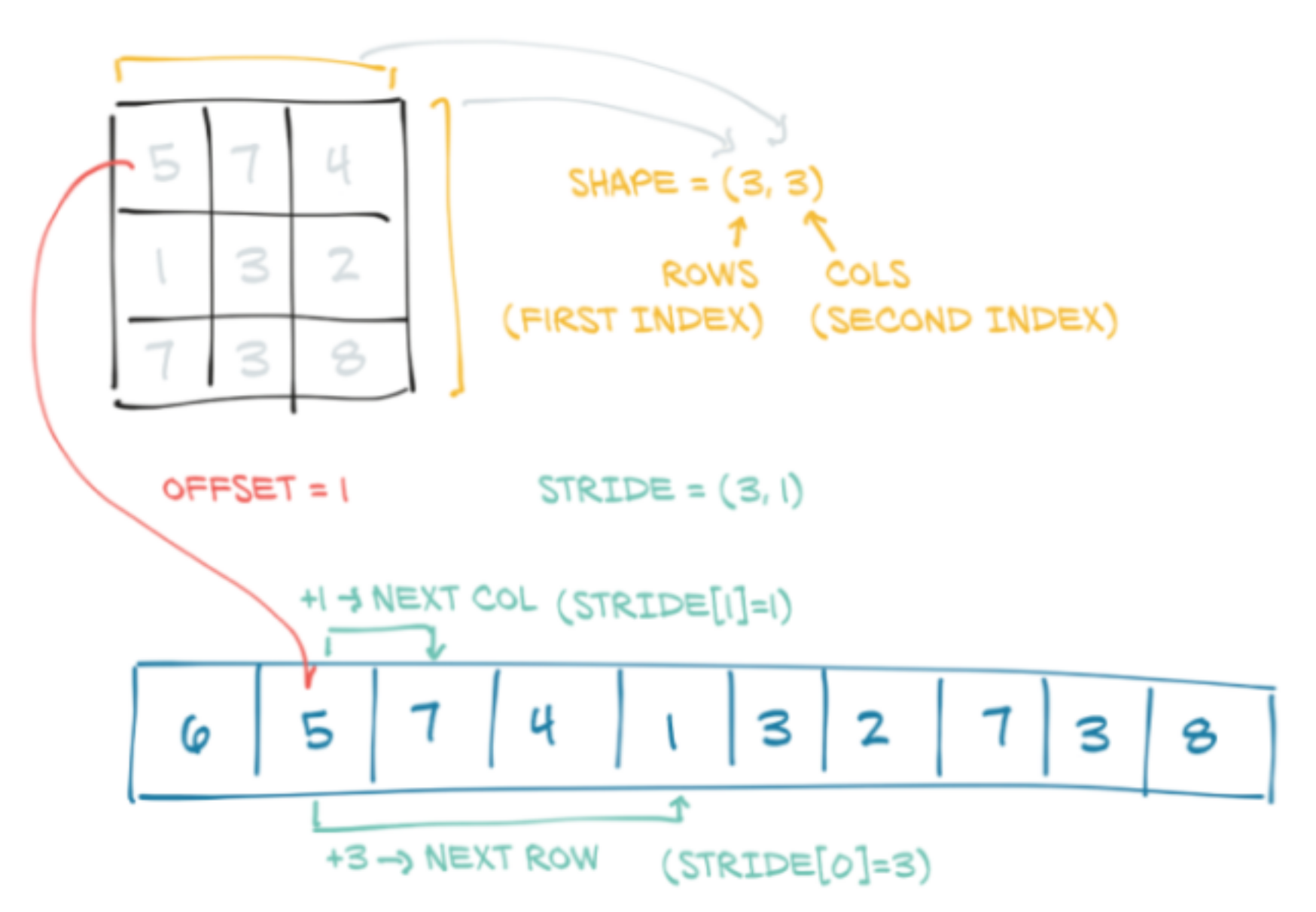
Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

Storage metadata

t.size()
t.storage_offset()
t.stride()
Output >>>
torch.Size([2, 5])
0
(5, 1)

size: (2, 5)
offset: 0
stride: (5, 1)

Storage metadata

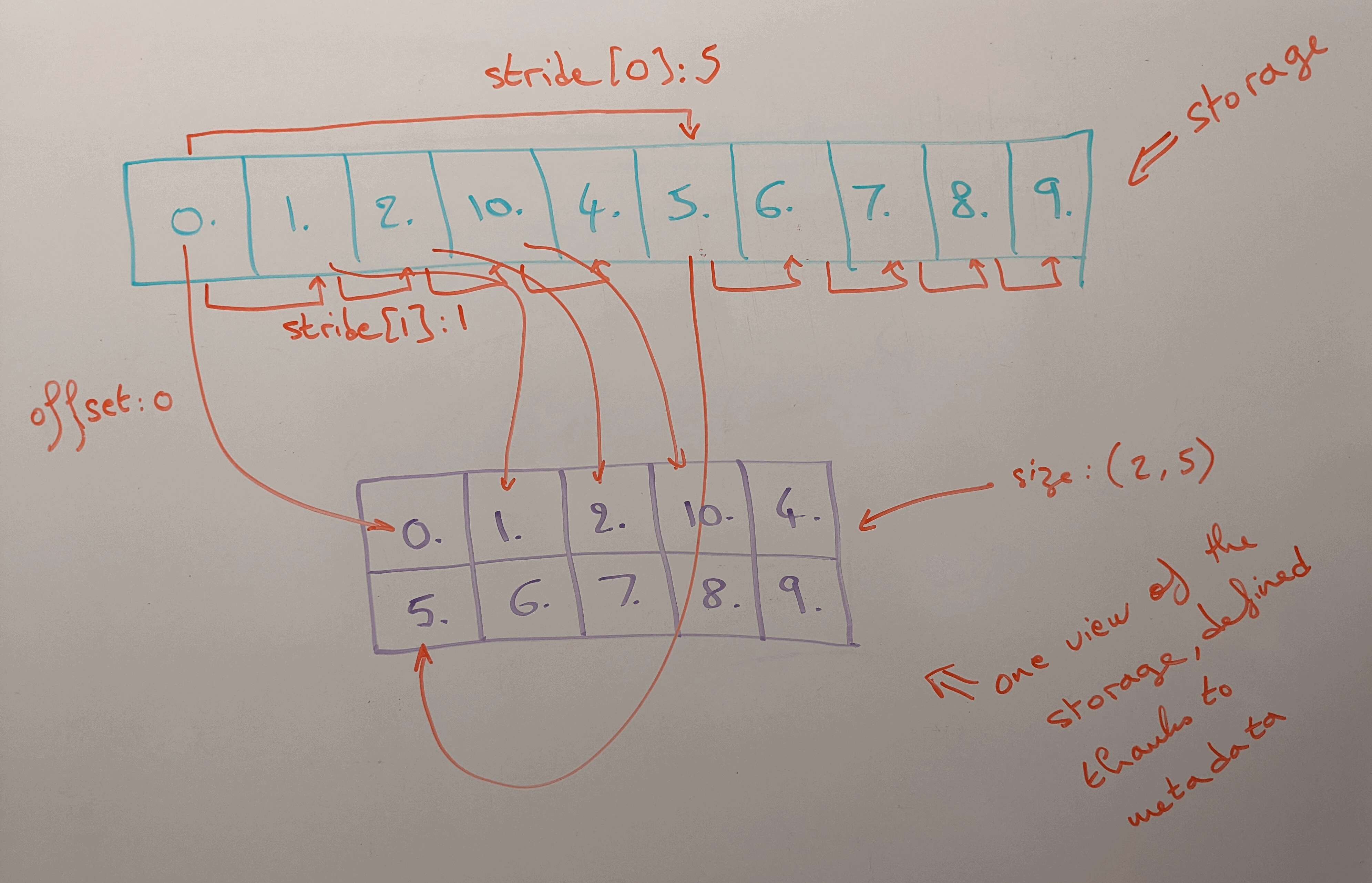
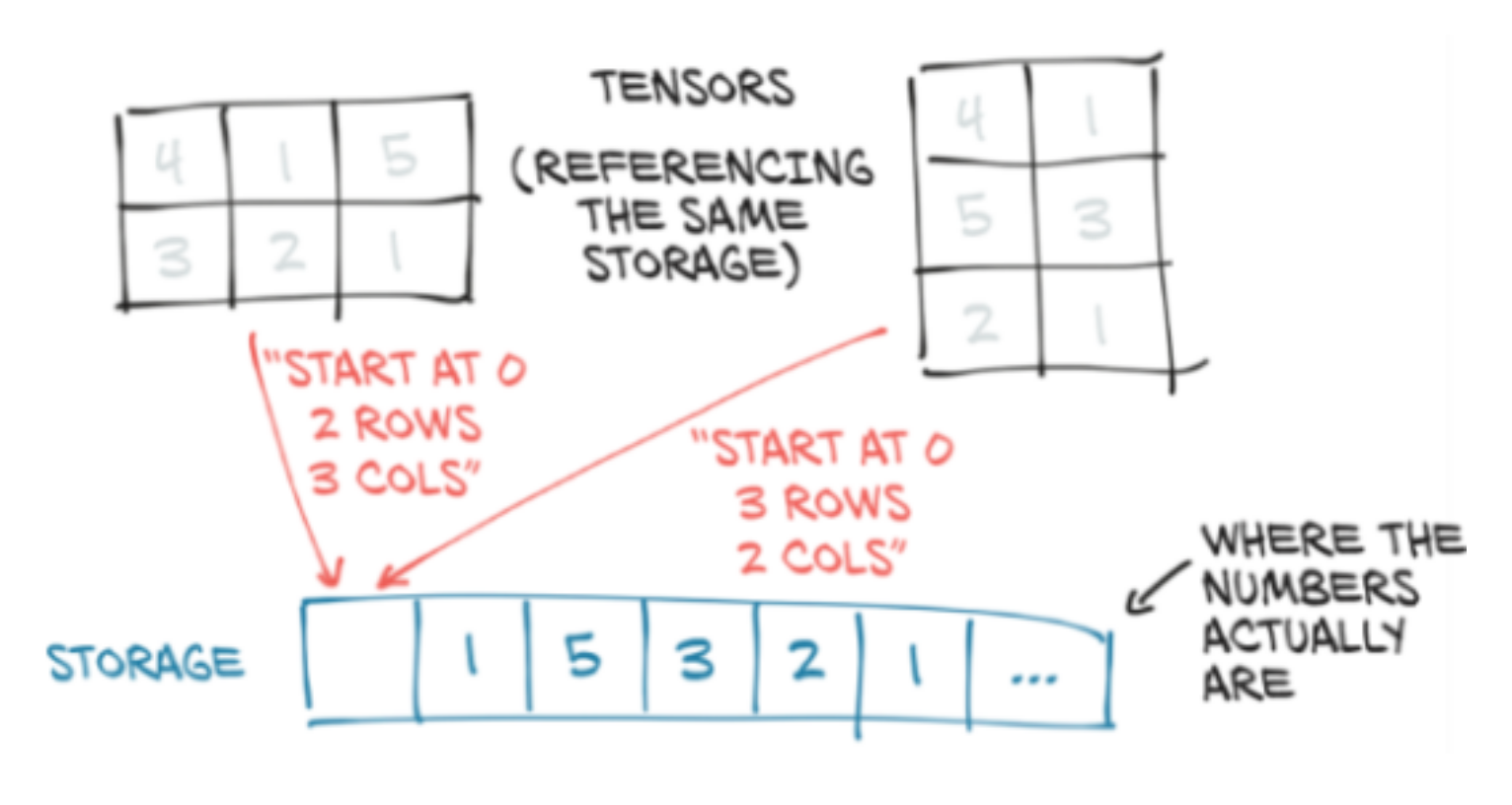
Sharing storage

Multiple tensors can use the same storage, saving a lot of memory since the metadata is a lot lighter than a whole new array

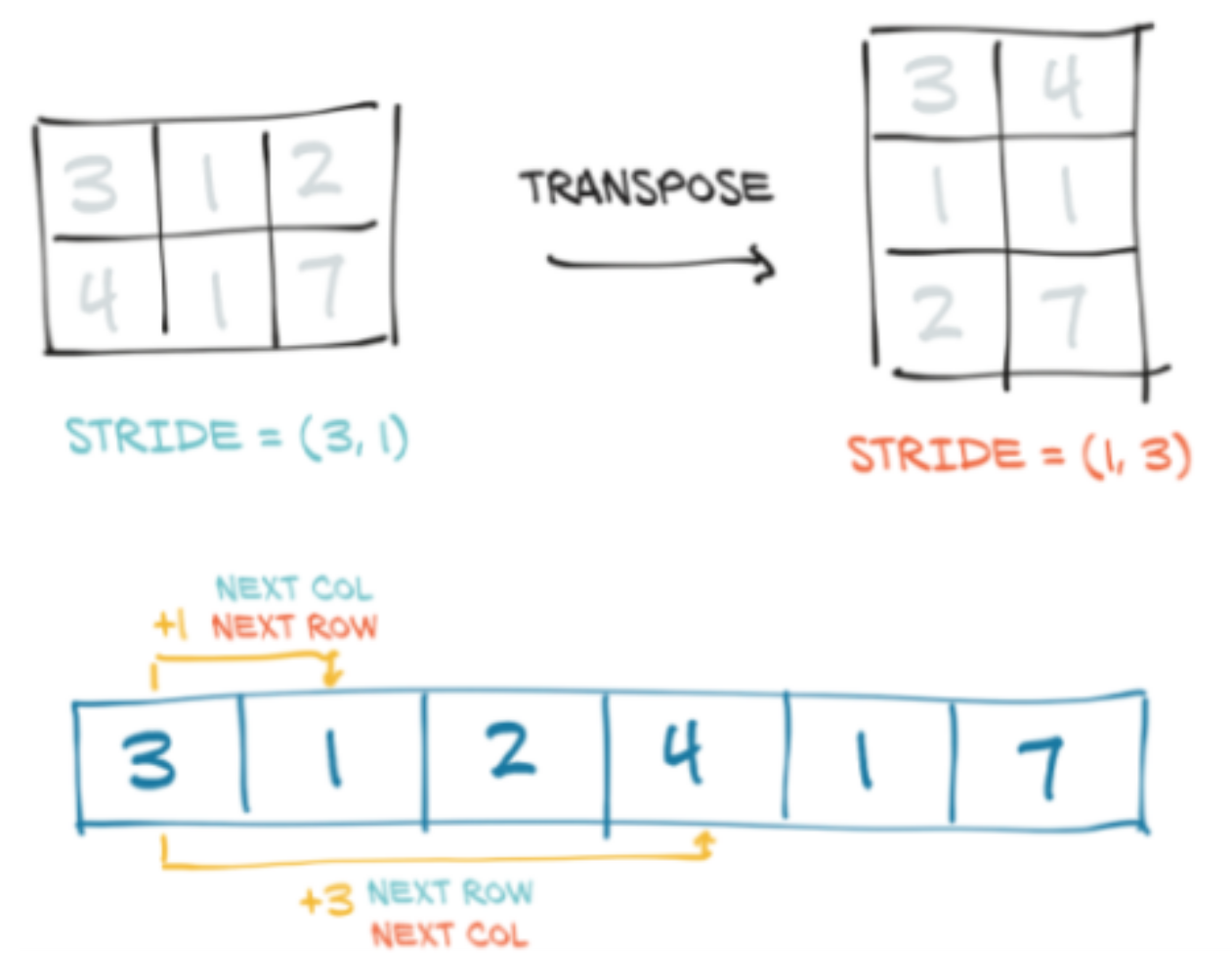
Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

Transposing in 2 dimensions

t = torch.tensor([[3, 1, 2], [4, 1, 7]]); print(t)
t.size()
t.t()
t.t().size()
Output >>>
tensor([[3, 1, 2],
        [4, 1, 7]])
torch.Size([2, 3])
tensor([[3, 4],
        [1, 1],
        [2, 7]])
torch.Size([3, 2])

Transposing in 2 dimensions

= flipping the stride elements around

Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications

Transposing in higher dimensions

torch.t() is a shorthand for torch.transpose(0, 1): 

torch.equal(t.t(), t.transpose(0, 1))
Output >>>
True

While torch.t() only works for 2D tensors, torch.transpose() can be used to transpose 2 dimensions in tensors of any number of dimensions

Transposing in higher dimensions

t = torch.zeros(1, 2, 3); print(t)

t.size()
t.stride()
Output >>>
tensor([[[0., 0., 0.],
         [0., 0., 0.]]])

torch.Size([1, 2, 3])
(6, 3, 1)

Transposing in higher dimensions

t.transpose(0, 1)

t.transpose(0, 1).size()
t.transpose(0, 1).stride()
Output >>>
tensor([[[0., 0., 0.]],
        [[0., 0., 0.]]])

torch.Size([2, 1, 3])
(3, 6, 1)  # Notice how transposing flipped 2 elements of the stride

Transposing in higher dimensions

t.transpose(0, 2)

t.transpose(0, 2).size()
t.transpose(0, 2).stride()
Output >>>
tensor([[[0.],
         [0.]],
        [[0.],
         [0.]],
        [[0.],
         [0.]]])

torch.Size([3, 2, 1])
(1, 3, 6)

Transposing in higher dimensions

t.transpose(1, 2)

t.transpose(1, 2).size()
t.transpose(1, 2).stride()
Output >>>
tensor([[[0., 0.],
         [0., 0.],
         [0., 0.]]])

torch.Size([1, 3, 2])
(6, 1, 3)

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

Default dtype

Since PyTorch tensors were built with utmost efficiency in mind for neural networks, the default data type is 32-bit floating points

This is sufficient for accuracy & much faster than 64-bit floating points

Note that, by contrast, NumPy ndarrays use 64-bit as their default

List of PyTorch tensor dtypes

torch.float16 / torch.half  16-bit / half-precision floating-point
torch.float32 / torch.float32-bit / single-precision floating-point
torch.float64 / torch.double64-bit / double-precision floating-point
torch.uint8unsigned 8-bit integers
torch.int8signed 8-bit integers
torch.int16 / torch.shortsigned 16-bit integers
torch.int32 / torch.intsigned 32-bit integers
torch.int64 / torch.longsigned 64-bit integers
torch.boolboolean

Checking & changing dtype

t = torch.rand(2, 3); print(t)
t.dtype   # Remember that the default dtype for PyTorch tensors is float32
t2 = t.type(torch.float64); print(t2) # If dtype ≠ default, it is printed
t2.dtype
Output >>>
tensor([[0.8130, 0.3757, 0.7682],
        [0.3482, 0.0516, 0.3772]])
torch.float32
tensor([[0.8130, 0.3757, 0.7682],
        [0.3482, 0.0516, 0.3772]], dtype=torch.float64)
torch.float64

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

Creating tensors

  • torch.tensor:     Input individual values
  • torch.arange:     Similar to range but creates a 1D tensor
  • torch.linspace:   1D linear scale tensor
  • torch.logspace:   1D log scale tensor
  • torch.rand:     Random numbers from a uniform distribution on [0, 1)
  • torch.randn:   Numbers from the standard normal distribution
  • torch.randperm:   Random permutation of integers
  • torch.empty:   Uninitialized tensor
  • torch.zeros:   Tensor filled with 0
  • torch.ones:     Tensor filled with 1
  • torch.eye:      Identity matrix

Creating tensors

torch.manual_seed(0)  # If you want to reproduce the result
torch.rand(1)

torch.manual_seed(0)  # Run before each operation to get the same result
torch.rand(1).item()  # Extract the value from a tensor
Output >>>
tensor([0.4963])

0.49625658988952637

Creating tensors

torch.rand(1)
torch.rand(1, 1)
torch.rand(1, 1, 1)
torch.rand(1, 1, 1, 1)
Output >>>
tensor([0.6984])
tensor([[0.5675]])
tensor([[[0.8352]]])
tensor([[[[0.2056]]]])

Creating tensors

torch.rand(2)
torch.rand(2, 2, 2, 2)
Output >>>
tensor([0.5932, 0.1123])
tensor([[[[0.1147, 0.3168],
          [0.6965, 0.9143]],
         [[0.9351, 0.9412],
          [0.5995, 0.0652]]],
        [[[0.5460, 0.1872],
          [0.0340, 0.9442]],
         [[0.8802, 0.0012],
          [0.5936, 0.4158]]]])

Creating tensors

torch.rand(2)
torch.rand(3)
torch.rand(1, 1)
torch.rand(1, 1, 1)
torch.rand(2, 6)
Output >>>
tensor([0.7682, 0.0885])
tensor([0.1320, 0.3074, 0.6341])
tensor([[0.4901]])
tensor([[[0.8964]]])
tensor([[0.4556, 0.6323, 0.3489, 0.4017, 0.0223, 0.1689],
        [0.2939, 0.5185, 0.6977, 0.8000, 0.1610, 0.2823]])

Creating tensors

torch.rand(2, 4, dtype=torch.float64)  # You can set dtype
torch.ones(2, 1, 4, 5)
Output >>>
tensor([[0.6650, 0.7849, 0.2104, 0.6767],
        [0.1097, 0.5238, 0.2260, 0.5582]], dtype=torch.float64)
tensor([[[[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]]],
        [[[1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1.]]]])

Creating tensors

t = torch.rand(2, 3); print(t)
torch.zeros_like(t)             # Matches the size of t
torch.ones_like(t)
torch.randn_like(t)
Output >>>
tensor([[0.4051, 0.6394, 0.0871],
        [0.4509, 0.5255, 0.5057]])
tensor([[0., 0., 0.],
        [0., 0., 0.]])
tensor([[1., 1., 1.],
        [1., 1., 1.]])
tensor([[-0.3088, -0.0104,  1.0461],
        [ 0.9233,  0.0236, -2.1217]])

Creating tensors

torch.arange(2, 10, 4)    # From 2 to 10 in increments of 4
torch.linspace(2, 10, 4)  # 4 elements from 2 to 10 on the linear scale
torch.logspace(2, 10, 4)  # Same on the log scale
torch.randperm(4)
torch.eye(3)
Output >>>
tensor([2, 6])
tensor([2.0000,  4.6667,  7.3333, 10.0000])
tensor([1.0000e+02, 4.6416e+04, 2.1544e+07, 1.0000e+10])
tensor([1, 3, 2, 0])
tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]])

Tensor information

t = torch.rand(2, 3); print(t)
t.size()
t.dim()
t.numel()
Output >>>
tensor([[0.5885, 0.7005, 0.1048],
        [0.1115, 0.7526, 0.0658]])
torch.Size([2, 3])
2
6

Tensor indexing

x = torch.rand(3, 4)
x[:]                 # With a range, the comma is implicit: same as x[:, ]
x[:, 2]
x[1, :]
x[2, 3]
Output >>>
tensor([[0.6575, 0.4017, 0.7391, 0.6268],
        [0.2835, 0.0993, 0.7707, 0.1996],
        [0.4447, 0.5684, 0.2090, 0.7724]])
tensor([0.7391, 0.7707, 0.2090])
tensor([0.2835, 0.0993, 0.7707, 0.1996])
tensor(0.7724)

Tensor indexing

x[-1:]        # Last element (implicit comma, so all columns)
x[-1]         # No range, no implicit comma: we are indexing 
# from a list of tensors, so the result is a one dimensional tensor
# (Each dimension is a list of tensors of the previous dimension)
x[-1].size()  # Same number of dimensions than x (2 dimensions)
x[-1:].size() # We dropped one dimension
Output >>>
tensor([[0.8168, 0.0879, 0.2642, 0.3777]])
tensor([0.8168, 0.0879, 0.2642, 0.3777])

torch.Size([4])
torch.Size([1, 4])

Tensor indexing

x[0:1]     # Python ranges are inclusive to the left, not the right
x[:-1]     # From start to one before last (& implicit comma)
x[0:3:2]   # From 0th (included) to 3rd (excluded) in increment of 2
Output >>>
tensor([[0.5873, 0.0225, 0.7234, 0.4538]])
tensor([[0.5873, 0.0225, 0.7234, 0.4538],
        [0.9525, 0.0111, 0.6421, 0.4647]])
tensor([[0.5873, 0.0225, 0.7234, 0.4538],
        [0.8168, 0.0879, 0.2642, 0.3777]])

Tensor indexing

x[None]          # Adds a dimension of size one as the 1st dimension
x.size()
x[None].size()
Output >>>
tensor([[[0.5873, 0.0225, 0.7234, 0.4538],
         [0.9525, 0.0111, 0.6421, 0.4647],
         [0.8168, 0.0879, 0.2642, 0.3777]]])
torch.Size([3, 4])
torch.Size([1, 3, 4])

A word of caution about indexing

While indexing elements of a tensor to extract some of the data as a final step of some computation is fine, you should not use indexing to run operations on tensor elements in a loop as this would be extremely inefficient Instead, you want to use vectorized operations

Vectorized operations

Since PyTorch tensors are homogeneous (i.e. made of a single data type), as with NumPy's ndarrays , operations are vectorized & thus staggeringly fast NumPy is mostly written in C & PyTorch in C++. With either library, when you run vectorized operations on arrays/tensors, you don’t use raw Python (slow) but compiled C/C++ code (much faster) Here is an excellent post explaining Python vectorization & why it makes such a big difference

Vectorized operations: comparison

Raw Python method

# Create tensor. We use float64 here to avoid truncation errors
t = torch.rand(10**6, dtype=torch.float64)
# Initialize the sum
sum = 0
# Run loop
for i in range(len(t)): sum += t[i]
# Print result
print(sum)

Vectorized function

t.sum()

Vectorized operations: comparison

Both methods give the same result

This is why we used float64:
While the accuracy remains excellent with float32 if we use the PyTorch function torch.sum(), the raw Python loop gives a fairly inaccurate result
Output >>>

tensor(500023.0789, dtype=torch.float64)

tensor(500023.0789, dtype=torch.float64)

Vectorized operations: timing

Let’s compare the timing with PyTorch built-in benchmark utility 

# Load utility
import torch.utils.benchmark as benchmark

# Create a function for our loop
def sum_loop(t, sum):
    for i in range(len(t)): sum += t[i]

Vectorized operations: timing

Now we can create the timers 

t0 = benchmark.Timer(
    stmt='sum_loop(t, sum)',
    setup='from __main__ import sum_loop',
    globals={'t': t, 'sum': sum})

t1 = benchmark.Timer(
    stmt='t.sum()',
    globals={'t': t})

Vectorized operations: timing

Let’s time 100 runs to have a reliable benchmark 

print(t0.timeit(100))
print(t1.timeit(100))

I ran the code on my laptop with a dedicated GPU & 32GB RAM

Vectorized operations: timing

Timing of raw Python loop

sum_loop(t, sum)
setup: from __main__ import sum_loop
  1.37 s
  1 measurement, 100 runs , 1 thread

Timing of vectorized function

t.sum()
  191.26 us
  1 measurement, 100 runs , 1 thread

Vectorized operations: timing

Speedup:

1.37/(191.26 * 10**-6) = 7163
The vectorized function runs more than 7,000 times faster!!!

Even more important on GPUs

We will talk about GPUs in detail later

Timing of raw Python loop on GPU (actually slower on GPU!) 

sum_loop(t, sum)
setup: from __main__ import sum_loop
  4.54 s
  1 measurement, 100 runs , 1 thread

Timing of vectorized function on GPU (here we do get a speedup)

t.sum()
  50.62 us
  1 measurement, 100 runs , 1 thread

Even more important on GPUs

Speedup:

4.54/(50.62 * 10**-6) = 89688

On GPUs, it is even more important not to index repeatedly from a tensor
On GPUs, the vectorized function runs almost 90,000 times faster!!!

Simple mathematical operations

t1 = torch.arange(1, 5).view(2, 2); print(t1)
t2 = torch.tensor([[1, 1], [0, 0]]); print(t2)
t1 + t2 # Operation performed between elements at corresponding locations
t1 + 1  # Operation applied to each element of the tensor
Output >>>
tensor([[1, 2],
        [3, 4]])
tensor([[1, 1],
        [0, 0]])
tensor([[2, 3],
        [3, 4]])
tensor([[2, 3],
        [4, 5]])

Reduction

t = torch.ones(2, 3, 4); print(t)
t.sum()   # Reduction over all entries
Output >>>
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],
        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])
tensor(24.)
Other reduction functions (e.g. mean) behave the same way

Reduction

# Reduction over a specific dimension
t.sum(0)  
t.sum(1)
t.sum(2)
Output >>>
tensor([[2., 2., 2., 2.],
        [2., 2., 2., 2.],
        [2., 2., 2., 2.]])
tensor([[3., 3., 3., 3.],
        [3., 3., 3., 3.]])
tensor([[4., 4., 4.],
        [4., 4., 4.]])

Reduction

# Reduction over multiple dimensions
t.sum((0, 1))
t.sum((0, 2))
t.sum((1, 2))
Output >>>
tensor([6., 6., 6., 6.])
tensor([8., 8., 8.])
tensor([12., 12.])

In-place operations

With operators post-fixed with _: 

t1 = torch.tensor([1, 2]); print(t1)
t2 = torch.tensor([1, 1]); print(t2)
t1.add_(t2); print(t1)
t1.zero_(); print(t1)
Output >>>
tensor([1, 2])
tensor([1, 1])
tensor([2, 3])
tensor([0, 0])

In-place operations vs reassignments

t1 = torch.ones(1); t1, hex(id(t1))
t1.add_(1); t1, hex(id(t1))        # In-place operation: same address
t1 = t1.add(1); t1, hex(id(t1))    # Reassignment: new address in memory
t1 = t1 + 1; t1, hex(id(t1))       # Reassignment: new address in memory
Output >>>
(tensor([1.]), '0x7fc61accc3b0')
(tensor([2.]), '0x7fc61accc3b0')
(tensor([3.]), '0x7fc61accc5e0')
(tensor([4.]), '0x7fc61accc6d0')

Tensor views

t = torch.tensor([[1, 2, 3], [4, 5, 6]]); print(t)
t.size()
t.view(6)
t.view(3, 2)
t.view(3, -1) # Same: with -1, the size is inferred from other dimensions
Output >>>
tensor([[1, 2, 3],
        [4, 5, 6]])
torch.Size([2, 3])
tensor([1, 2, 3, 4, 5, 6])
tensor([[1, 2],
        [3, 4],
        [5, 6]])

Note the difference

t1 = torch.tensor([[1, 2, 3], [4, 5, 6]]); print(t1)
t2 = t1.t(); print(t2)
t3 = t1.view(3, 2); print(t3)
Output >>>
tensor([[1, 2, 3],
        [4, 5, 6]])
tensor([[1, 4],
        [2, 5],
        [3, 6]])
tensor([[1, 2],
        [3, 4],
        [5, 6]])

Logical operations

t1 = torch.randperm(5); print(t1)
t2 = torch.randperm(5); print(t2)
t1 > 3                            # Test each element
t1 < t2                           # Test corresponding pairs of elements
Output >>>
tensor([4, 1, 0, 2, 3])
tensor([0, 4, 2, 1, 3])
tensor([ True, False, False, False, False])
tensor([False,  True,  True, False, False])

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

Conversion without copy

PyTorch tensors can be converted to NumPy ndarrays & vice-versa in a very efficient manner as both objects share the same memory 

t = torch.rand(2, 3); print(t)
t_np = t.numpy(); print(t_np)      # From PyTorch tensor to NumPy ndarray
Output >>>
tensor([[0.8434, 0.0876, 0.7507],
        [0.1457, 0.3638, 0.0563]])   # PyTorch Tensor

[[0.84344184 0.08764815 0.7506627 ]
 [0.14567494 0.36384273 0.05629885]] # NumPy ndarray

Mind the different defaults

t_np.dtype
Output >>>
dtype('float32')

Remember that PyTorch tensors use 32-bit floating points by default
(because this is what you want in neural networks)

But NumPy defaults to 64-bit
Depending on your workflow, you might have to change dtype

From NumPy to PyTorch

import numpy as np
a = np.random.rand(2, 3); print(a)
a_pt = torch.from_numpy(a); print(a_pt)    # From ndarray to tensor
Output >>>
[[0.55892276 0.06026952 0.72496545]
 [0.65659463 0.27697739 0.29141587]]

tensor([[0.5589, 0.0603, 0.7250],
        [0.6566, 0.2770, 0.2914]], dtype=torch.float64)
Here again, you might have to change dtype

Notes about conversion without copy

t & t_np are objects of different Python types, so, as far as Python is concerned, they have different addresses 

id(t) == id(t_np)
Output >>>
False

Notes about conversion without copy

However—that's quite confusing —they share an underlying C array in memory & modifying one in-place also modifies the other 

t.zero_()
print(t_np)
Output >>>
tensor([[0., 0., 0.],
        [0., 0., 0.]])

[[0. 0. 0.]
 [0. 0. 0.]]

Notes about conversion without copy

Lastly, as NumPy only works on CPU, to convert a PyTorch tensor allocated to the GPU, the content will have to be copied to the CPU first

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

  • All functions from numpy.linalg implemented
    (with accelerator & automatic differentiation support)

  • Some additional functions

Requires torch >= 1.9
Linear algebra support was less developed before the introduction of this module

System of linear equations solver

Let’s have a look at an extremely basic example:

2x + 3y - z = 5
x - 2y + 8z = 21
6x + y - 3z = -1

We are looking for the values of x, y, & z that would satisfy this system

System of linear equations solver

We create a 2D tensor A of size (3, 3) with the coefficients of the equations
& a 1D tensor b of size 3 with the right hand sides values of the equations 

A = torch.tensor([[2., 3., -1.], [1., -2., 8.], [6., 1., -3.]]); print(A)
b = torch.tensor([5., 21., -1.]); print(b)
Output >>>
tensor([[ 2.,  3., -1.],
        [ 1., -2.,  8.],
        [ 6.,  1., -3.]])
tensor([ 5., 21., -1.])

System of linear equations solver

Solving this system is as simple as running the torch.linalg.solve function:

x = torch.linalg.solve(A, b); print(x)
Output >>>
tensor([1., 2., 3.])

Our solution is:

x = 1
y = 2
z = 3

Verify our result

torch.allclose(A @ x, b)
Output >>>
True

System of linear equations solver

Here is another simple example: 

# Create a square normal random matrix
A = torch.randn(4, 4); print(A)
# Create a tensor of right hand side values
b = torch.randn(4); print(b)

# Solve the system
x = torch.linalg.solve(A, b); print(x)

# Verify
torch.allclose(A @ x, b)

System of linear equations solver

Output >>>
tensor([[ 1.5091,  2.0820,  1.7067,  2.3804], # A (coefficients)
        [-1.1256, -0.3170, -1.0925, -0.0852],
        [ 0.3276, -0.7607, -1.5991,  0.0185],
        [-0.7504,  0.1854,  0.6211,  0.6382]])

tensor([-1.0886, -0.2666,  0.1894, -0.2190])  # b (right hand side values)

tensor([ 0.1992, -0.7011,  0.2541, -0.1526])  # x (our solution)

True									      # Verification

With 2 multidimensional tensors

A = torch.randn(2, 3, 3)              # Must be batches of square matrices
B = torch.randn(2, 3, 5)              # Dimensions must be compatible
X = torch.linalg.solve(A, B); print(X)
torch.allclose(A @ X, B)
Output >>>
tensor([[[-0.0545, -0.1012,  0.7863, -0.0806, -0.0191],
         [-0.9846, -0.0137, -1.7521, -0.4579, -0.8178],
         [-1.9142, -0.6225, -1.9239, -0.6972,  0.7011]],
        [[ 3.2094,  0.3432, -1.6604, -0.7885,  0.0088],
         [ 7.9852,  1.4605, -1.7037, -0.7713,  2.7319],
         [-4.1979,  0.0849,  1.0864,  0.3098, -1.0347]]])
True

Matrix inversions

It is faster & more numerically stable to solve a system of linear equations directly than to compute the inverse matrix first
Limit matrix inversions to situations where it is truly necessary

Matrix inversions

A = torch.rand(2, 3, 3)      # Batch of square matrices
A_inv = torch.linalg.inv(A)  # Batch of inverse matrices
A @ A_inv                    # Batch of identity matrices
Output >>>
tensor([[[ 1.0000e+00, -6.0486e-07,  1.3859e-06],
         [ 5.5627e-08,  1.0000e+00,  1.0795e-06],
         [-1.4133e-07,  7.9992e-08,  1.0000e+00]],
        [[ 1.0000e+00,  4.3329e-08, -3.6741e-09],
         [-7.4627e-08,  1.0000e+00,  1.4579e-07],
         [-6.3580e-08,  8.2354e-08,  1.0000e+00]]])

Other linear algebra functions

torch.linalg contains many more functions:

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

Device attribute

Tensor data can be placed in the memory of various processor types:

Device attribute

The values for the device attributes are:

  • CPU:  'cpu'

  • GPU (CUDA & AMD’s ROCm):  'cuda'

  • XLA:  xm.xla_device()

This last option requires to load the torch_xla package first:

import torch_xla
import torch_xla.core.xla_model as xm

Creating a tensor on a specific device

By default, tensors are created on the CPU 

t1 = torch.rand(2); print(t1)
Output >>>
tensor([0.1606, 0.9771])  # Implicit: device='cpu'
Printed tensors only display attributes with values ≠ default values

Creating a tensor on a specific device

You can create a tensor on an accelerator by specifying the device attribute 

t2_gpu = torch.rand(2, device='cuda'); print(t2_gpu)
Output >>>
tensor([0.0664, 0.7829], device='cuda:0')  # :0 means the 1st GPU

Copying a tensor to a specific device

You can also make copies of a tensor on other devices 

# Make a copy of t1 on the GPU
t1_gpu = t1.to(device='cuda'); print(t1_gpu)
t1_gpu = t1.cuda()  # Same as above written differently

# Make a copy of t2_gpu on the CPU
t2 = t2_gpu.to(device='cpu'); print(t2)
t2 = t2_gpu.cpu()   # For the altenative form
Output >>>
tensor([0.1606, 0.9771], device='cuda:0')
tensor([0.0664, 0.7829]) # Implicit: device='cpu'

Multiple GPUs

If you have multiple GPUs, you can optionally specify which one a tensor should be created on or copied to 

t3_gpu = torch.rand(2, device='cuda:0')  # Create a tensor on 1st GPU
t4_gpu = t1.to(device='cuda:0')          # Make a copy of t1 on 1st GPU
t5_gpu = t1.to(device='cuda:1')          # Make a copy of t1 on 2nd GPU

Or the equivalent short forms for the last two: 

t4_gpu = t1.cuda(0)
t5_gpu = t1.cuda(1)

Timing

Let’s compare the timing of some matrix multiplications on CPU & GPU with PyTorch built-in benchmark utility 

# Load utility
import torch.utils.benchmark as benchmark
# Define tensors on the CPU
A = torch.randn(500, 500)
B = torch.randn(500, 500)
# Define tensors on the GPU
A_gpu = torch.randn(500, 500, device='cuda')
B_gpu = torch.randn(500, 500, device='cuda')
I ran the code on my laptop with a dedicated GPU & 32GB RAM

Timing

Let’s time 100 runs to have a reliable benchmark 

t0 = benchmark.Timer(
    stmt='A @ B',
    globals={'A': A, 'B': B})

t1 = benchmark.Timer(
    stmt='A_gpu @ B_gpu',
    globals={'A_gpu': A_gpu, 'B_gpu': B_gpu})

print(t0.timeit(100))
print(t1.timeit(100))

Timing

Output >>>
A @ B
  2.29 ms
  1 measurement, 100 runs , 1 thread

A_gpu @ B_gpu
  108.02 us
  1 measurement, 100 runs , 1 thread

Speedup:

(2.29 * 10**-3)/(108.02 * 10**-6) = 21

This computation was 21 times faster on my GPU than on CPU

Timing

By replacing 500 with 5000, we get:

A @ B
  2.21 s
  1 measurement, 100 runs , 1 thread

A_gpu @ B_gpu
  57.88 ms
  1 measurement, 100 runs , 1 thread

Speedup:

2.21/(57.88 * 10**-3) = 38

The larger the computation, the greater the benefit: now 38 times faster

- What is a PyTorch tensor?

- Memory storage

- Data type (dtype)

- Basic operations

- Working with NumPy

- Linear algebra

- Harvesting the power of GPUs

- Distributed operations

Parallel tensor operations

PyTorch already allows for distributed training of ML models

The implementation of distributed tensor operations—for instance for linear algebra—is in the work through the use of a ShardedTensor primitive that can be sharded across nodes

See also this issue for more comments about upcoming developments on (among other things) tensor sharding

Questions?