Super-resolution with PyTorch
Marie-Hélène Burle
Marie-Hélène Burle
training@westgrid.ca
November 24, 2021

Definitions
LR: low resolution
HR: high resolution
SR: super-resolution = reconstruction of HR images from LR images
SISR: single-image super-resolution = SR using a single input image
History of super-resolution
Can be broken down into 2 main periods:
A rather slow history with various interpolation algorithms of increasing complexity before deep neural networks
An incredibly fast evolution since the advent of deep learning (DL)
SR history Pre-DL
Pixel-wise interpolation prior to DL
Various methods ranging from simple (e.g. nearest-neighbour , bicubic ) to complex (e.g. Gaussian process regression , iterative FIR Wiener filter ) algorithms
SR history Pre-DL
Nearest-neighbour interpolation
Simplest method of interpolation
Simply uses the value of the nearest pixel
Bicubic interpolation
Consists of determining the 16 coefficients
SR history with DL
Deep learning has seen a fast evolution marked by the successive emergence of various frameworks and architectures over the past 10 years
Some key network architectures and frameworks:
- CNN
- GAN
- Transformers
These have all been applied to SR
SR history with DL
SR using (amongst others):
Convolutional Neural Networks (SRCNN) — 2014
Random Forests — 2015
Perceptual loss — 2016
Sub-pixel CNN — 2016
ResNet (SRResNet) & Generative Adversarial Network (SRGAN) — 2017
Enhanced SRGAN (ESRGAN) — 2018
Predictive Filter Flow (PFF) — 2018
Densely Residual Laplacian attention Network (DRLN) — 2019
Second-order Attention Network (SAN) — 2019
Learned downscaling with Content Adaptive Resampler (CAR) — 2019
Holistic Attention Network (HAN) — 2020
Swin Transformer — 2021
SRCNN
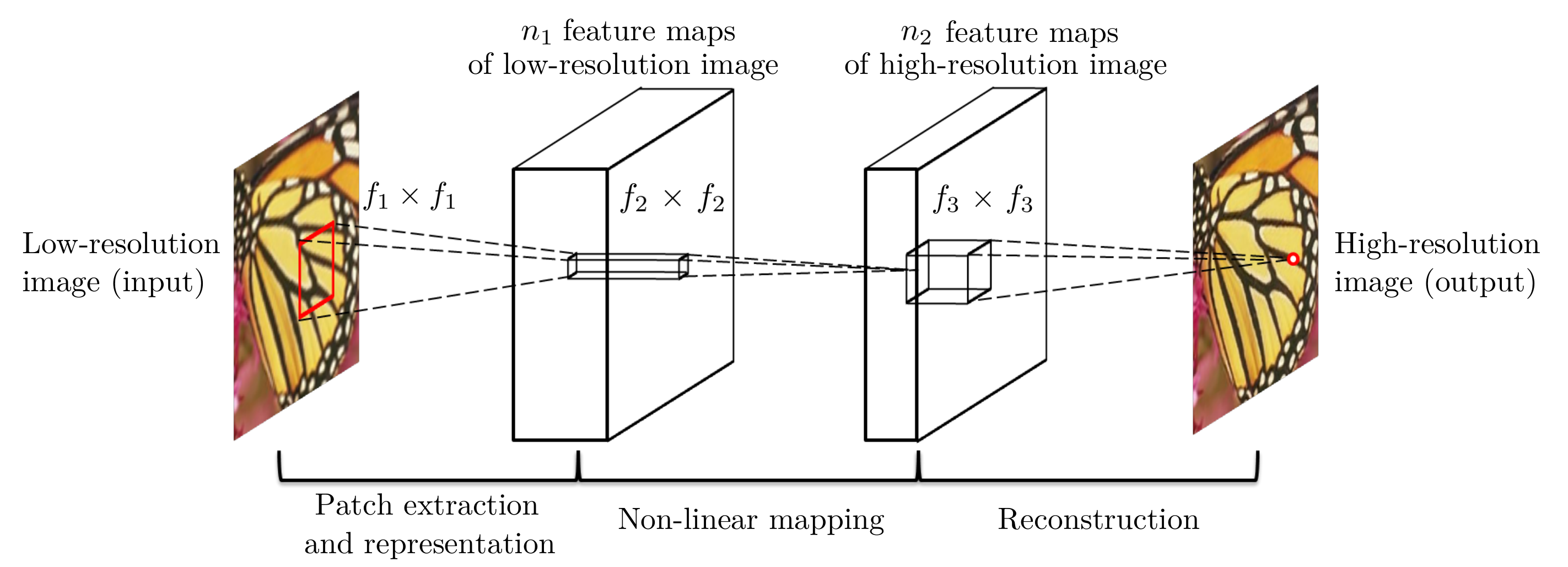
Dong, C., Loy, C. C., He, K., & Tang, X. (2015). Image super-resolution using deep convolutional networks. IEEE transactions on pattern analysis and machine intelligence, 38(2), 295-307
Given a low-resolution image Y, the first convolutional layer of the SRCNN extracts a set of feature maps. The second layer maps these feature maps nonlinearly to high-resolution patch representations. The last layer combines the predictions within a spatial neighbourhood to produce the final high-resolution image F(Y)
SRCNN
Can use sparse-coding-based methods
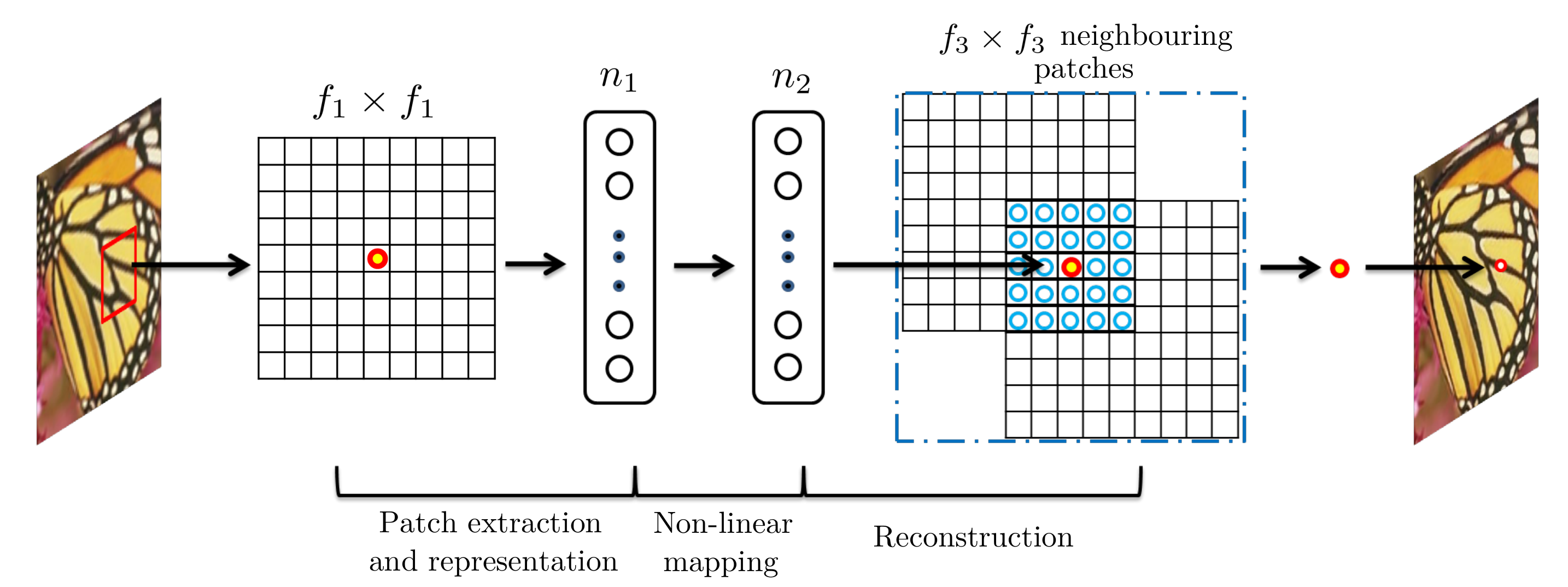
Dong, C., Loy, C. C., He, K., & Tang, X. (2015). Image super-resolution using deep convolutional networks. IEEE transactions on pattern analysis and machine intelligence, 38(2), 295-307
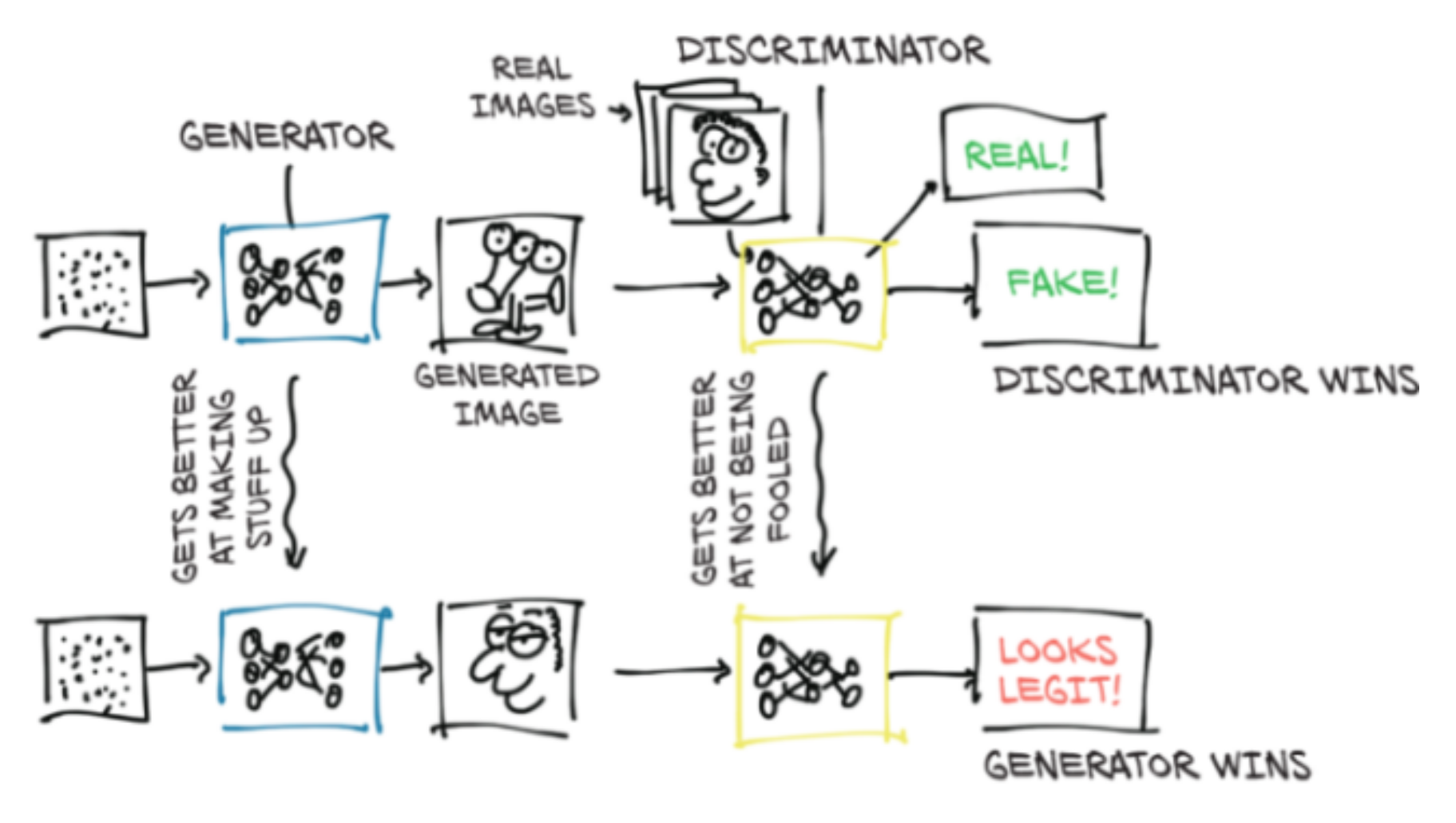
SRGAN
Do not provide the best PSNR, but can give more realistic results by providing more texture (less smoothing)
GAN
SRGAN
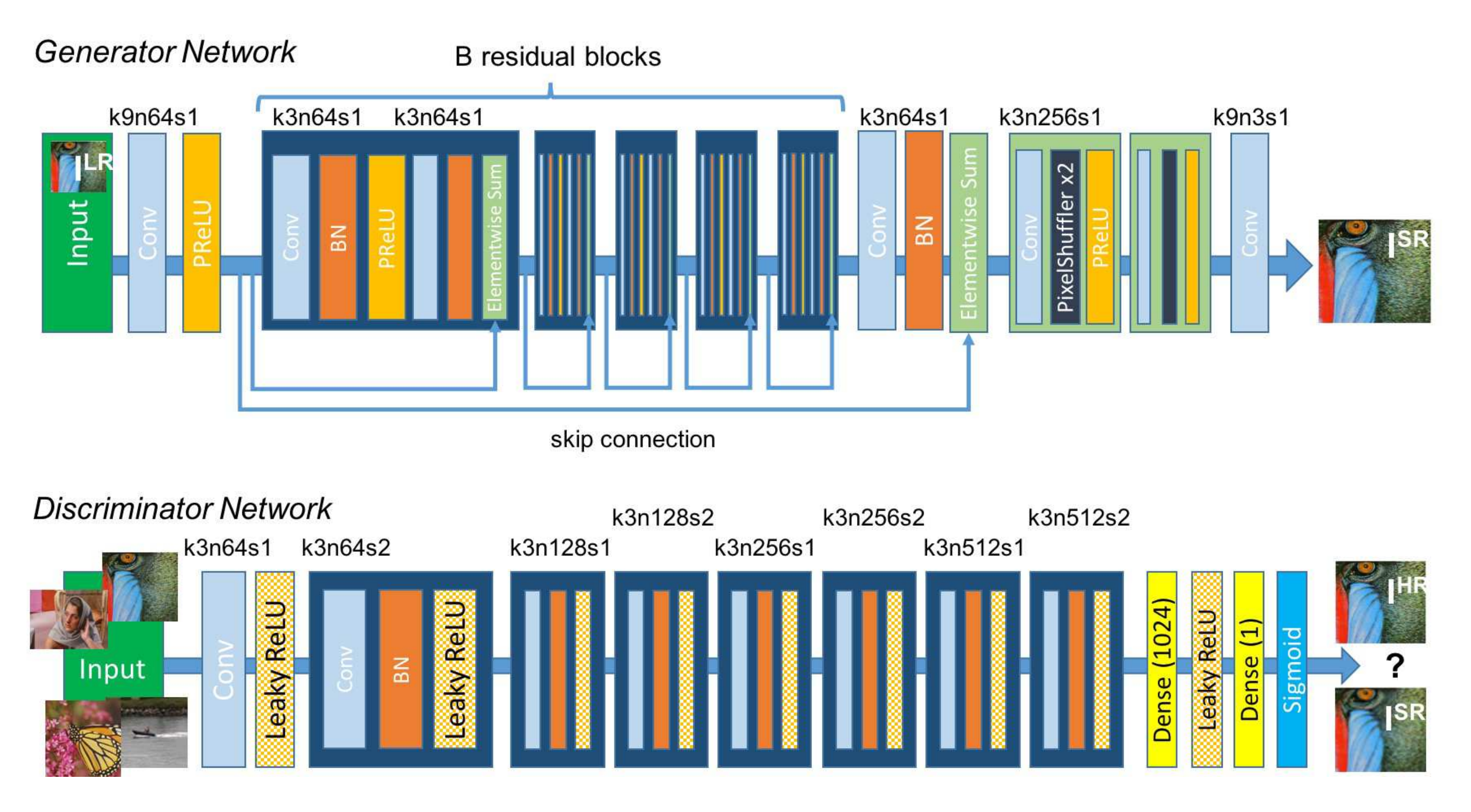
Ledig, C., Theis, L., Huszár, F., Caballero, J., Cunningham, A., Acosta, A., … & Shi, W. (2017). Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 4681-4690)
SRGAN
Followed by the ESRGAN and many other flavours of SRGANs
SwinIR
Attention
(cited 2769 times)
(cited 30999 times…)
Transformers

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008)
Transformers
Initially used for NLP to replace RNN as they allow parallelization Now entering the domain of vision and others Very performant with relatively few parameters
Swin Transformer
The Swin Transformer improved the use of transformers to the vision domain
Swin = Shifted WINdows
Swin Transformer
Swin transformer (left) vs transformer as initially applied to vision (right):
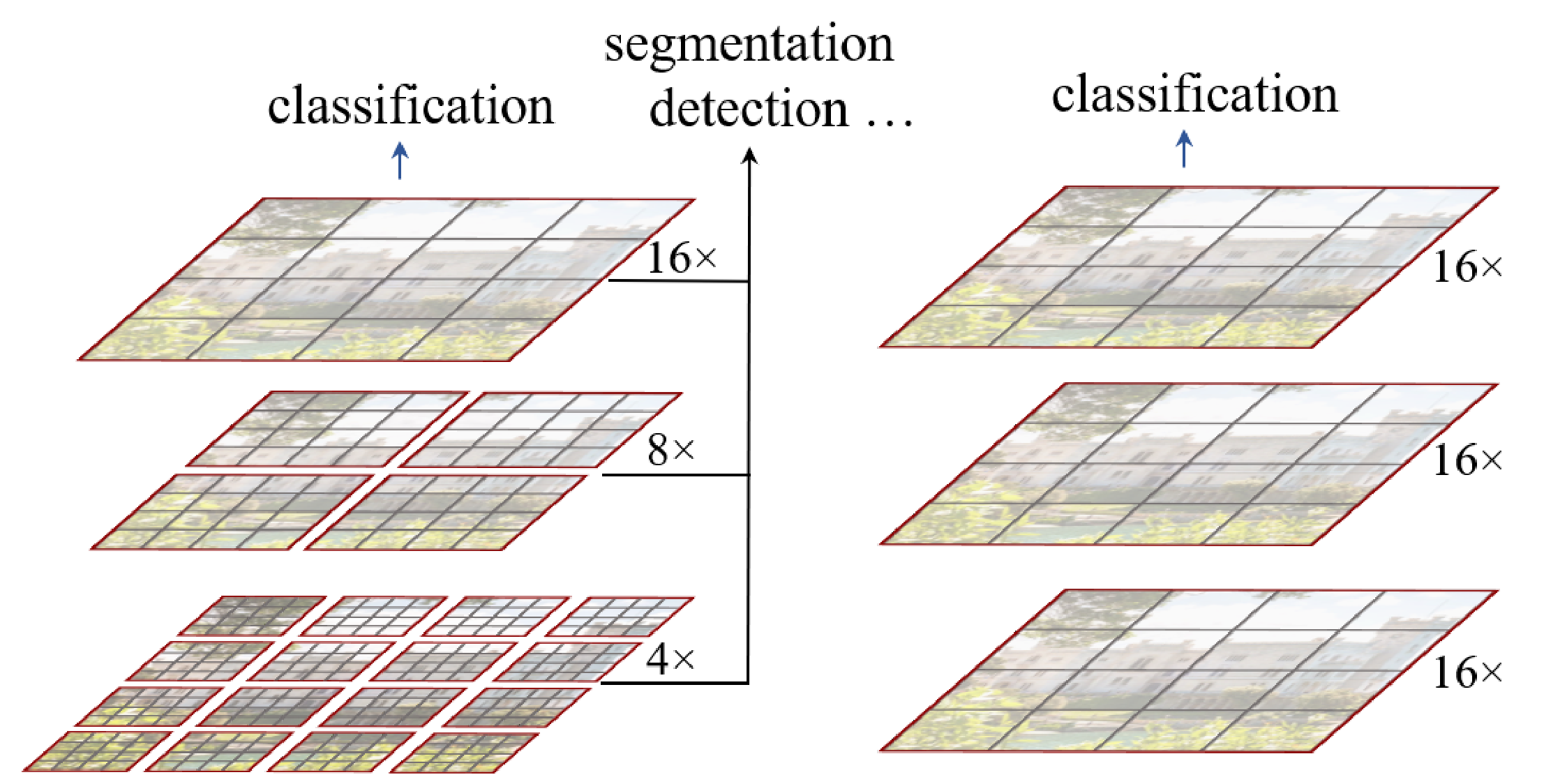
Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., … & Guo, B. (2021). Swin transformer: Hierarchical vision transformer using shifted windows. arXiv preprint arXiv:2103.14030
SwinIR
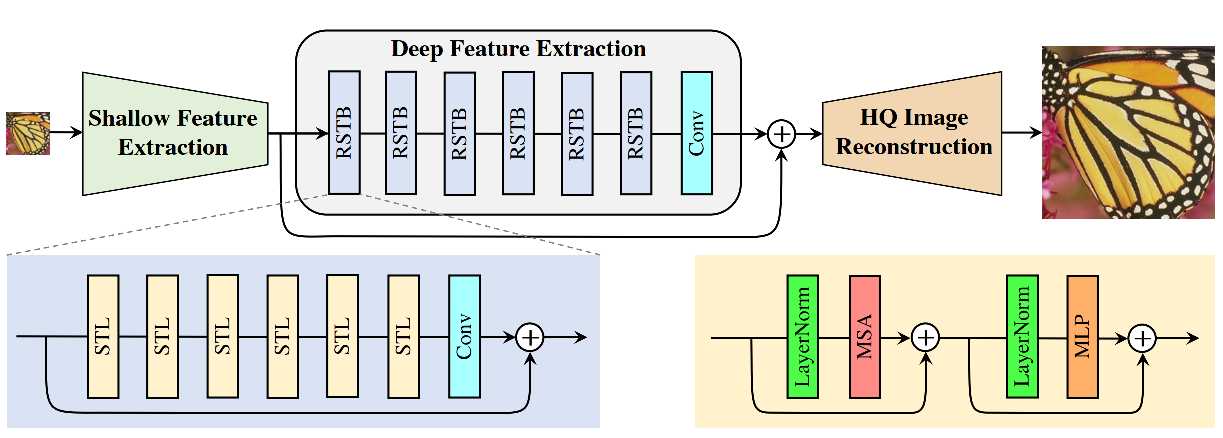
Liang, J., Cao, J., Sun, G., Zhang, K., Van Gool, L., & Timofte, R. (2021). SwinIR: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 1833-1844)
Training sets used
DIV2K , Flickr2K, and other datasets
Models assessment
3 metrics commonly used:
Peak sign-to-noise ratio (PSNR) measured in dB
Structural similarity index measure (SSIM)
Prediction of perceived image quality based on a “perfect” reference image
Mean opinion score (MOS)
Mean of subjective quality ratings
Models assessment
Peak sign-to-noise ratio (PSNR) measured in dB
Structural similarity index measure (SSIM)
Mean opinion score (MOS)
Metrics implementation
Metrics implementation
Metrics implementation
import kornia
psnr_value = kornia.metrics.psnr(input, target, max_val)
ssim_value = kornia.metrics.ssim(img1, img2, window_size, max_val=1.0, eps=1e-12)See the Kornia documentation for more info on kornia.metrics.psnr & kornia.metrics.ssim
Benchmark datasets
Set5

Set14

BSD100 (Berkeley Segmentation Dataset)

Benchmark datasets
Set5

Set14

BSD100 (Berkeley Segmentation Dataset)

The Set5 dataset
A dataset consisting of 5 images which has been used for at least 18 years to assess SR methods
How to get the dataset?
From the HuggingFace Datasets Hub with the HuggingFace datasets package:
from datasets import load_dataset
set5 = load_dataset('eugenesiow/Set5', 'bicubic_x4', split='validation')Dataset exploration
print(set5)
len(set5)
set5[0]
set5.shape
set5.column_names
set5.features
set5.set_format('torch', columns=['hr', 'lr'])
set5.formatBenchmarks
A 2012 review of interpolation methods for SR gives the metrics for a series of interpolation methods (using other datasets)
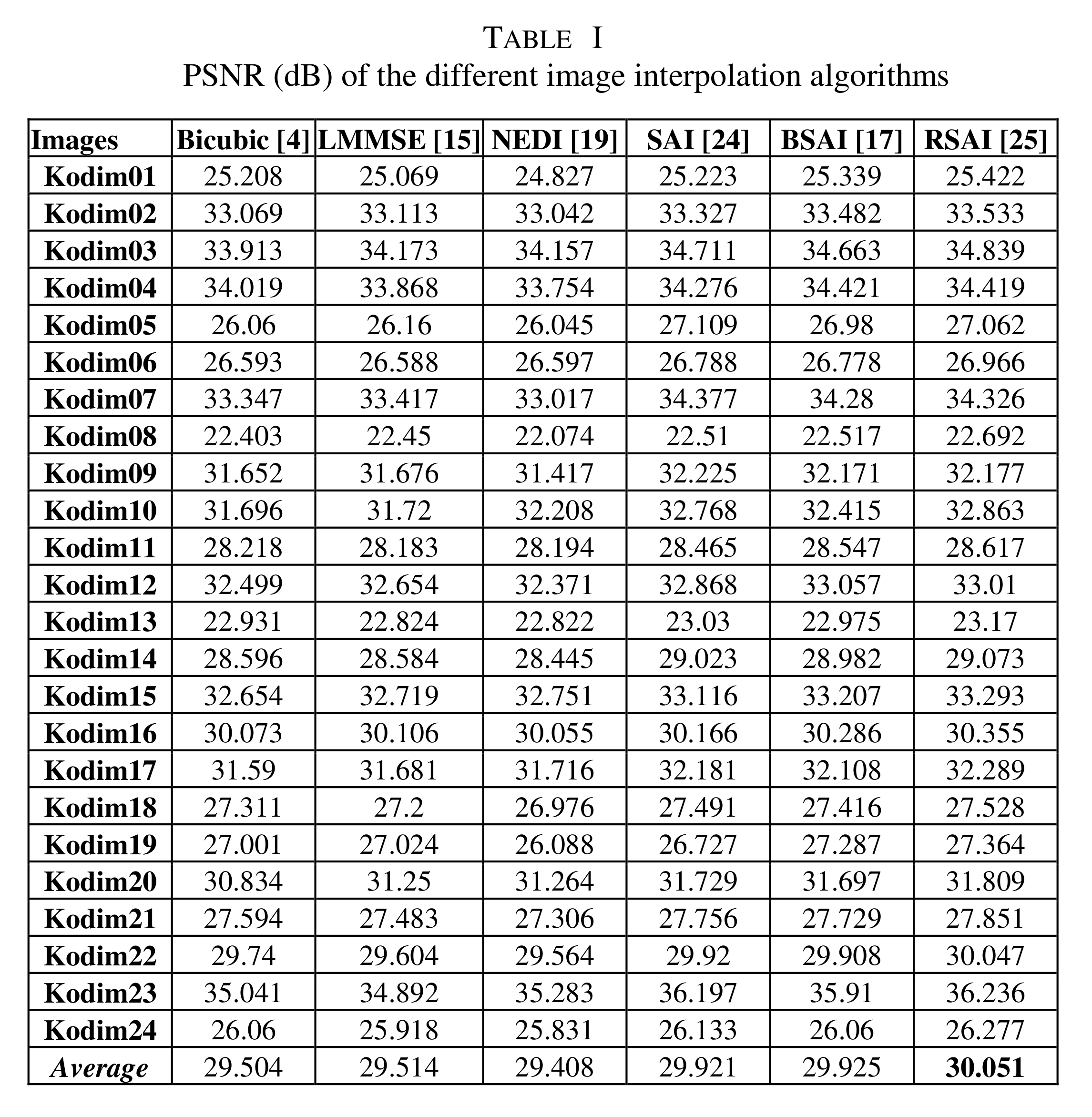


Interpolation methods



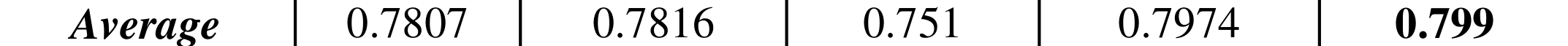
DL methods
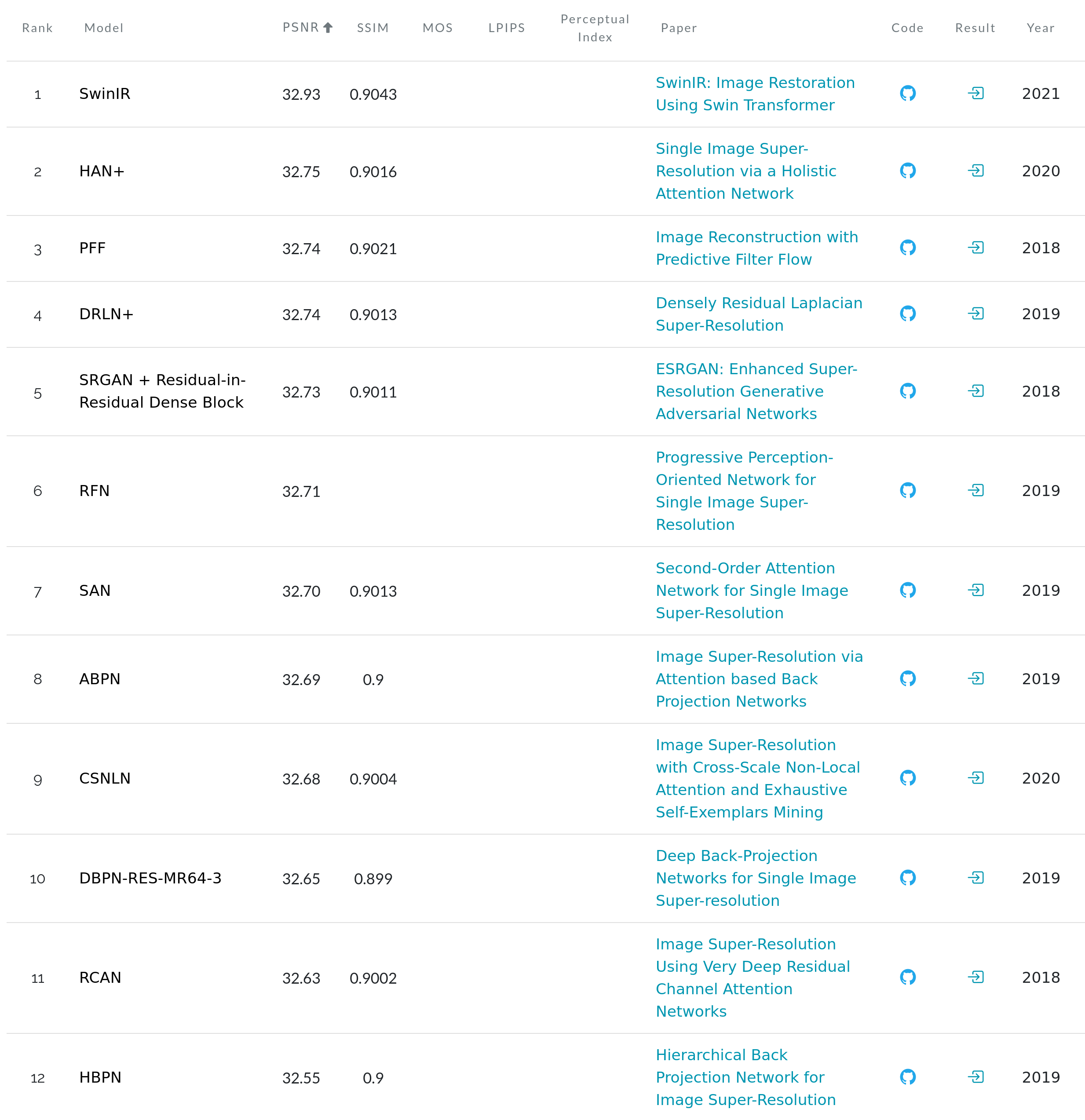
PSNR vs number of parameters for different methods on Set5x4

Liang, J., Cao, J., Sun, G., Zhang, K., Van Gool, L., & Timofte, R. (2021). SwinIR: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 1833-1844)
Comparison between SwinIR & a representative CNN-based model (RCAN) on classical SR images x4
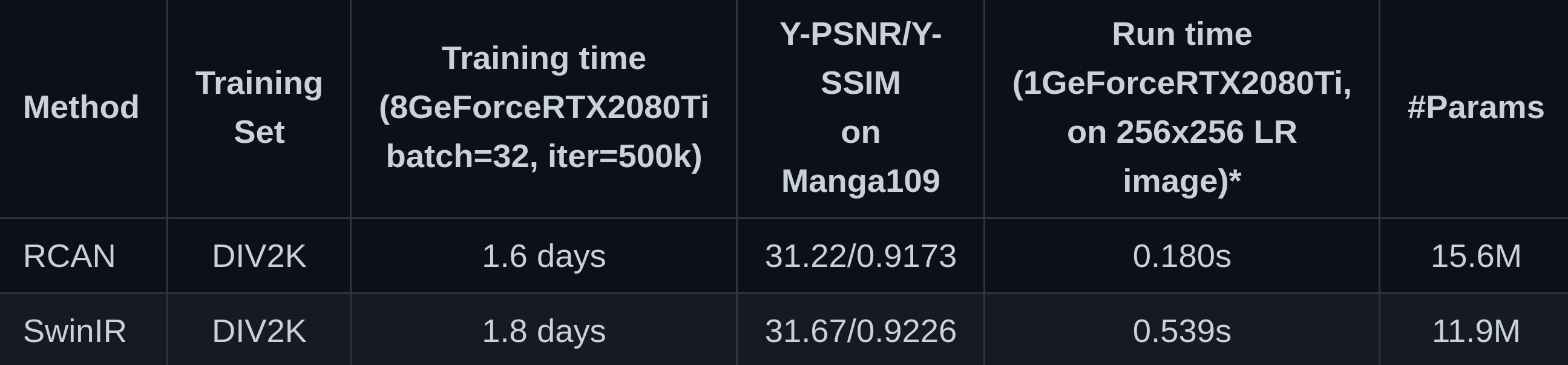
Liang, J., Cao, J., Sun, G., Zhang, K., Van Gool, L., & Timofte, R. (2021). SwinIR: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 1833-1844)
Comparison between SwinIR & a representative CNN-based model (RCAN) on classical SR images x4

Liang, J., Cao, J., Sun, G., Zhang, K., Van Gool, L., & Timofte, R. (2021). SwinIR: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 1833-1844)

Let’s use SwinIR
# Get the model
git clone git@github.com:JingyunLiang/SwinIR.git
cd SwinIR
# Copy our test images in the repo
cp -r <some/path>/my_tests /testsets/my_tests
# Run the model on our images
python main_test_swinir.py --tile 400 --task real_sr --scale 4 --large_model --model_path model_zoo/swinir/003_realSR_BSRGAN_DFOWMFC_s64w8_SwinIR-L_x4_GAN.pth --folder_lq testsets/my_testsRan in 9 min on my machine with one GPU and 32GB of RAM
Results


Results


Results


Results


Results


Results


Results


Results


Results


Results


Metrics
We could use the PSNR and SSIM implementations from SwinIR , but let’s try the Kornia functions we mentioned earlier:
Metrics
Let’s load the libraries we need:
import kornia
from PIL import Image
import torch
from torchvision import transformsMetrics
Then, we load one pair images (LR and HR):
berlin1_lr = Image.open("<some/path>/lr/berlin_1945_1.jpg")
berlin1_hr = Image.open("<some/path>/hr/berlin_1945_1.png")We can display these images with:
berlin1_lr.show()
berlin1_hr.show()Metrics
Now, we need to resize them so that they have identical dimensions and turn them into tensors:
preprocess = transforms.Compose([
transforms.Resize(256),
transforms.ToTensor()
])
berlin1_lr_t = preprocess(berlin1_lr)
berlin1_hr_t = preprocess(berlin1_hr)Metrics
berlin1_lr_t.shape
berlin1_hr_t.shapetorch.Size([3, 267, 256])
torch.Size([3, 267, 256])We now have tensors with 3 dimensions:
- the channels (RGB)
- the height of the image (in pixels)
- the width of the image (in pixels)
Metrics
As data processing is done in batch in ML, we need to add a 4th dimension: the batch size
(It will be equal to 1 since we have a batch size of a single image)
batch_berlin1_lr_t = torch.unsqueeze(berlin1_lr_t, 0)
batch_berlin1_hr_t = torch.unsqueeze(berlin1_hr_t, 0)Metrics
Our new tensors are now ready:
batch_berlin1_lr_t.shape
batch_berlin1_hr_t.shapetorch.Size([1, 3, 267, 256])
torch.Size([1, 3, 267, 256])PSNR
psnr_value = kornia.metrics.psnr(batch_berlin1_lr_t, batch_berlin1_hr_t, max_val=1.0)
psnr_value.item()33.379642486572266SSIM
ssim_map = kornia.metrics.ssim(batch_berlin1_lr_t, batch_berlin1_hr_t, window_size=5, max_val=1.0, eps=1e-12)
ssim_map.mean().item()0.9868119359016418